数据结构
1. 数组和链表的区别?
从逻辑结构上来看,数组必须实现定于固定的长度,不能适应数据动态增减的情况,即数组的大小一旦定义就不能改变。当数据增加是,可能超过原先定义的元素的个数;当数据减少时,造成内存浪费;链表动态进行存储分配,可以适应数据动态地增减的情况,且可以方便地插入、删除数据项。
从内存存储的角度看;数组从栈中分配空间(用new则在堆上创建),对程序员方便快速,但是自由度小;链表从堆中分配空间,自由度大但是申请管理比较麻烦。
从访问方式类看,数组在内存中是连续的存储,因此可以利用下标索引进行访问;链表是链式存储结构,在访问元素时候只能够通过线性方式由前到后顺序的访问,所以访问效率比数组要低。
2. 简述快速排序过程
[!NOTE] 掌握所有常见的排序算法的手写实现,以及复杂度相关细节知识。
选择一个基准元素,通常选择第一个元素或者最后一个元素,
通过一趟排序将待排序的记录分割成独立的两部分,其中一部分记录的元素值均比基准元素值小。另一部分记录的元素值比基准值大。
此时基准元素在其排好序后的正确位置
然后分别对这两部分记录用同样的方法继续进行排序,直到整个序列有序。
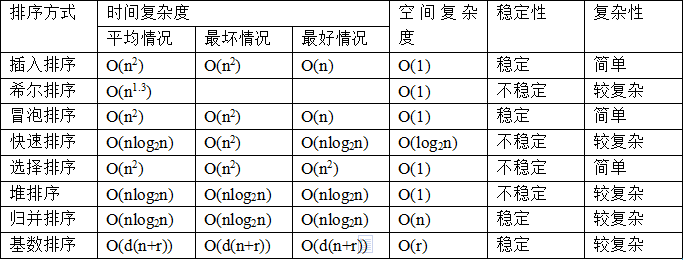
3. 各类排序算法对比(熟练掌握)
3.1 时间复杂度来说
平方阶(O(n2))排序 各类简单排序:直接插入、直接选择和冒泡排序;
线性对数阶(O(nlog2n))排序 快速排序、堆排序和归并排序;
O(n1+§))排序,§是介于0和1之间的常数。 希尔排序
- 线性阶(O(n))排序 基数排序,此外还有桶、箱排序。
说明:
当原表有序或基本有序时,直接插入排序和冒泡排序将大大减少比较次数和移动记录的次数,时间复杂度可降至O(n);
而快速排序则相反,当原表基本有序时,将蜕化为冒泡排序,时间复杂度提高为O(n2);
原表是否有序,对简单选择排序、堆排序、归并排序和基数排序的时间复杂度影响不大。
3.2 稳定性
[!NOTE] 排序算法的稳定性:若待排序的序列中,存在多个具有相同关键字的记录,经过排序,这些记录的相对次序保持不变,则称该算法是稳定的;若经排序后,记录的相对次序发生了改变,则称该算法是不稳定的。
3.2.1 稳定的排序算法
冒泡排序、插入排序、归并排序和基数排序
3.2.2 不是稳定的排序算法
选择排序、快速排序、希尔排序、堆排序
3.3 选择排序算法准则
一般而言,需要考虑的因素有以下四点:
设待排序元素的个数为n.
当n较大,则应采用时间复杂度为O(nlog2n)的排序方法:快速排序、堆排序或归并排序序。
当n较大,内存空间允许,且要求稳定性:归并排序
当n较小,可采用直接插入或直接选择排序。
直接插入排序:当元素分布有序,直接插入排序将大大减少比较次数和移动记录的次数。
直接选择排序 :元素分布有序,如果不要求稳定性,选择直接选择排序
一般不使用或不直接使用传统的冒泡排序。
基数排序 它是一种稳定的排序算法,但有一定的局限性:
- 关键字可分解。
- 记录的关键字位数较少,如果密集更好
- 如果是数字时,最好是无符号的
4. 解决哈希冲突的方法(面试重点)
[!NOTE] 需要对HashTable的底层实现有深入的理解,知道哈希冲突的产生原因和解决方法。
哈希表(Hash table,也叫散列表),是根据关键码值(Key value)而直接进行访问的数据结构。
1) 线性探测法
2) 平方探测法
3) 伪随机序列法
4) 拉链法
5. B树(了解)
[!NOTE] 如果对数据库有了解的话,该知识点需要深入理解。
根据B类树的特点,构造一个多阶的B类树,然后在尽量多的在结点上存储相关的信息,保证层数尽量的少,以便后面我们可以更快的找到信息,磁盘的I/O操作也少一些,而且B类树是平衡树,每个结点到叶子结点的高度都是相同,这也保证了每个查询是稳定的。
B树和B+树的区别,以一个m阶树为例。
关键字的数量不同;B+树中分支结点有m个关键字,其叶子结点也有m个,其关键字只是起到了一个索引的作用,但是B树虽然也有m个子结点,但是其只拥有m-1个关键字。
存储的位置不同;B+树中的数据都存储在叶子结点上,也就是其所有叶子结点的数据组合起来就是完整的数据,但是B树的数据存储在每一个结点中,并不仅仅存储在叶子结点上。
分支结点的构造不同;B+树的分支结点仅仅存储着关键字信息和儿子的指针(这里的指针指的是磁盘块的偏移量),也就是说内部结点仅仅包含着索引信息。
查询不同;B树在找到具体的数值以后,则结束,而B+树则需要通过索引找到叶子结点中的数据才结束,也就是说B+树的搜索过程中走了一条从根结点到叶子结点的路径。